Reference: Gilbert Strang、寺田、Github笔记
🧧支持偷偷✨:[置顶]⬆️修考使用必看🔥
1)方程组的几何解释📐
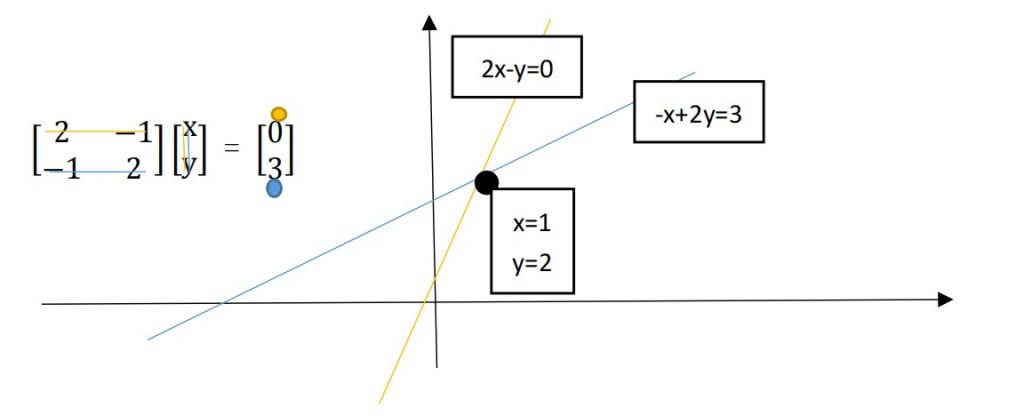
行图像就是在系数矩阵(coefficient matrix)上面,一次取一行构成方程,在坐标系上面作图,但是如果推广到高维的时候,做图就会变得异常的困难!
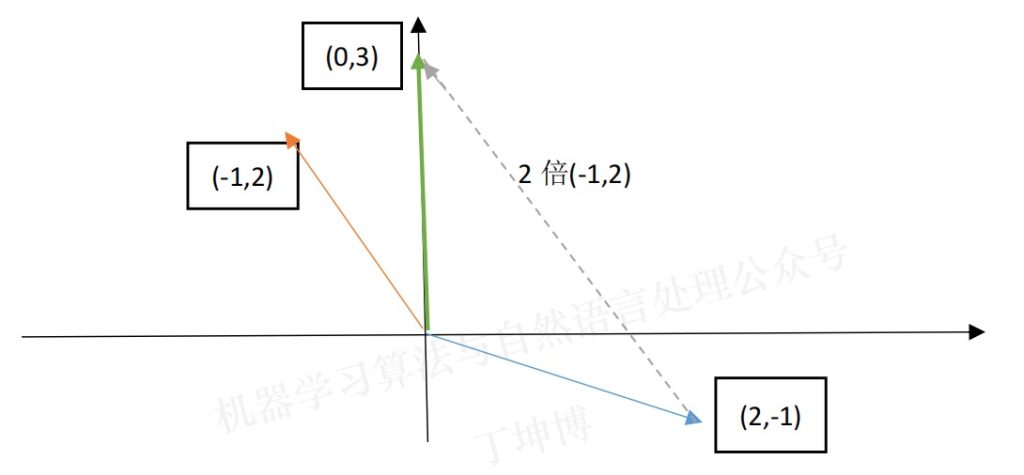
列图像就是在系数矩阵中把方程按列提取,然后寻找线性组合得到右边的结果。
所以,列图像远比行图像简便许多!
在找列图像的线性组合是否有解的时候,就要考虑列向量的能否覆盖三维空间。
矩阵乘法,可以看作是列向量的组合或是行向量的组合

2)矩阵消元
矩阵消元法:类比初中方程组,想办法把系数矩阵化成上三角形U,用增广矩阵化简
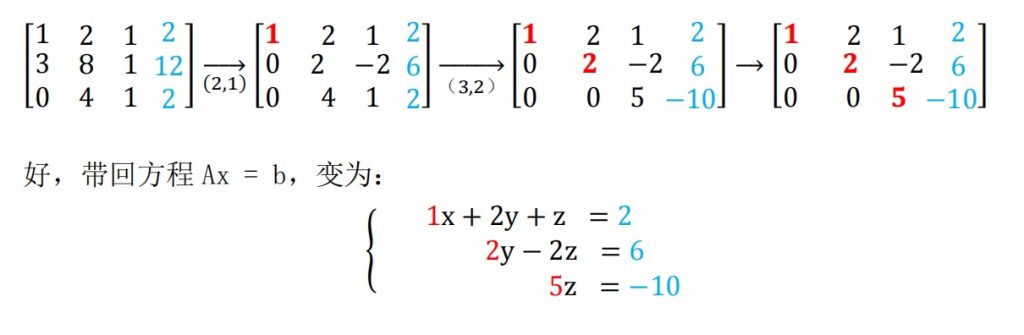
行列式的左乘是行变换,右乘是列变换

3)乘法和逆矩阵
矩阵乘法:一行✖️一列
行组合与列组合:类比上面,简单来说就是拓展了维度。
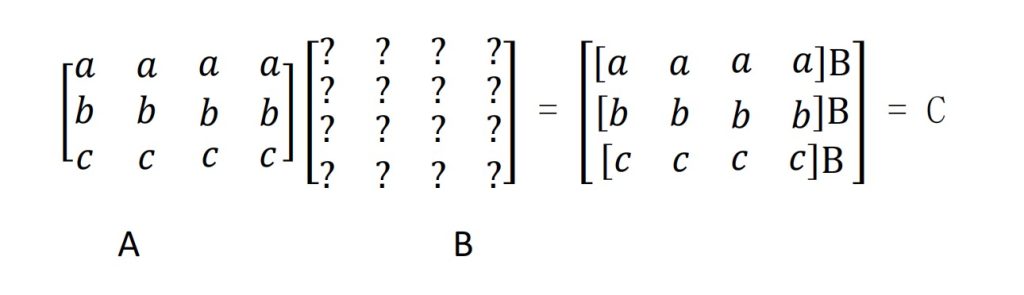
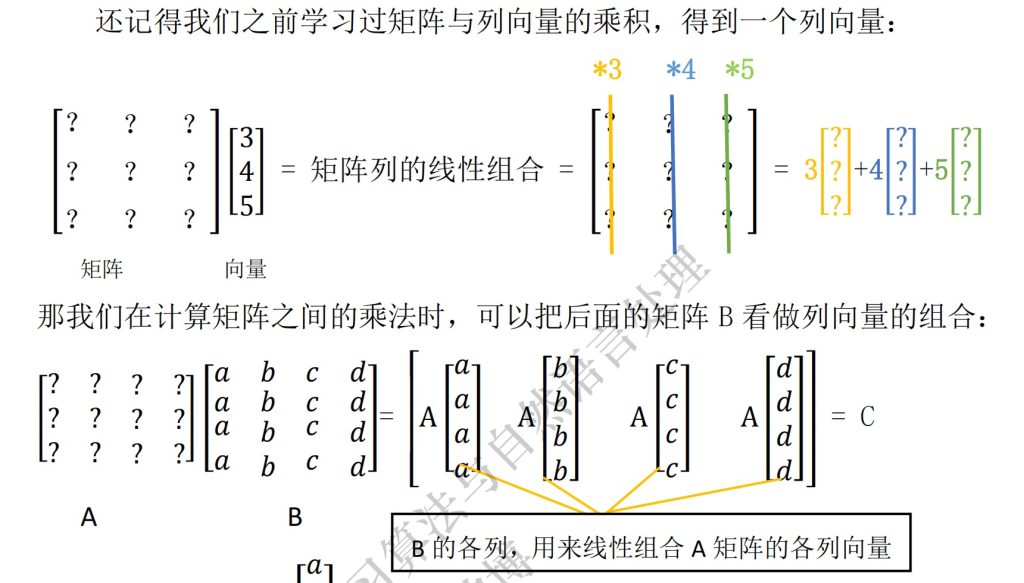
分块乘法:只要划分的大小匹配!
逆矩阵(inverse matrix):有如下结论⬇️

逆矩阵求解❓:可以用高斯-若尔当方法,简要来说就是化简[A | I]的增广矩阵为[I | A^-1],原理就是虚线右边的部份在化简的时候经历了和左边同样的行变换过程。
补充:(AB)^-1 = B^-1 * A^-1
4)A的LU分解
简单来说就是把A分成一个下三角L✖️上三角U

5)转置-转换-向量空间R
转置矩阵:直观理解,行元素和列元素交换。

向量空间:也就是该空间对线性运算(相加、数乘)封闭
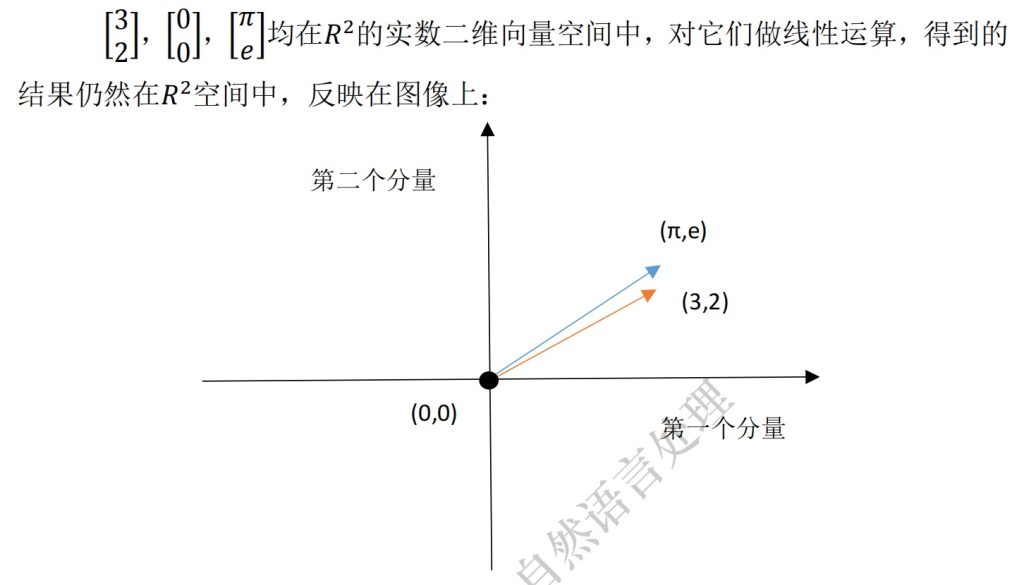
6)列空间和零空间
子空间对并运算不封闭(分别取一个向量然后做加法运算,会脱离范围),对交运算封闭(做加法、数乘都在空间内)

⬆️图也可以解释为找到A的列向量的线性组合可以构成b,也就是使得Ax= b有解
零空间:就是Ax = 0的所有解构成的一个空间。任何一个向量集合中必须要有零向量。如果解集里没有零向量,那根本构不成零空间。

7)求解Ax = 0, 主变量,特解
找零空间的时候,先化简找秩-->找出主元和自由变量-->给自由变量赋值(1和0交替)--> 回带求解
8)Ax=b的可解性和解的结构
Ax = b这个方程不一定有解,一般做法就是化简增广矩阵做判断。
我们从本题中得到一个启示:Ax = b 有解的条件:
·列空间角度:当且仅当 b 属于 A 的列空间时成立
·线性组合角度:b 必须是 A 各列的线性组合。
·A 矩阵本身变换角度:如果 A 的各行线性组合得到零行(如例【1】),那么对b 取相同运算方式,必将得到自然数 0
Ax = b方程的通解 = 矩阵零空间向量 + 矩阵特解(注意带上不定系数C1、C2……)
有解的情况仔细看下面文档📄⬇️
9)线性相关性、基、维数
在线性代数里,向量空间的一组元素中,若没有向量可用有限个其他向量的线性组合所表示,则称为线性无关或线性独立(linearly independent),反之称为线性相关(linearly dependent)。
零空间从秩的角度看来:
·线性无关对应向量组构成的矩阵,秩为 n,此时没有自由变量,零空间中
只有零向量存在。
·线性相关对应向量组构成的矩阵,秩小于 n,有 n-r 个自由变量,零空间
中有很多向量。
零空间维数 = n - r,所谓零空间维数,即是零空间基的个数,也是 Ax = 0 的特解的个数,
还可以理解为:Ax = 0 的解中自由变量的个数
10)四个基本子空间
这章内容非常抽象和偏理解❗️仔细阅读📖
11)矩阵空间、秩1矩阵
秩为1的矩阵可以分解成一列✖️一行
那么从空间角度看,所有秩为 4 的矩阵构成的集合 M,能称之为空间么?肯定不是。其中都不包含零向量。两个秩为 4 的矩阵相加,结果的秩可能大于 4。所以所有秩为 4 的矩阵集合并不能构成空间(违反了向量空间的封闭性)。同理,秩为 1 的矩阵集合也不能构成空间。
12)矩阵应用:图与网络
就是关联矩阵之类的应用
13)复习
零空间:Ax = 0成立的所有解向量构成的空间
矩阵A右乘列向量可以理解为对A各列向量的线性组合
存在除零矩阵以外平方为零的矩阵
这些空间真的很抽象😭
14)正交向量与子空间
零空间与行空间是正交的
需要注意:A*At不一定是可逆的!!只能说明它是一个方阵;要根据秩来判断。
15)子空间投影
投影矩阵:设b投影在a的向量为p = xa, 然后可以推出一个投影矩阵p。注意:aat与ata是不同的!如果a为列向量,前者是一个矩阵,后者是一个具体的数字。如果投影两次,结果还是不变(直观理解P的性质)
向量在平面上的投影,也就是设矩阵形式的方程,然后来求解。(也要注意只有AtA是可逆的,要左乘他们的逆!!)
16)投影矩阵和最小二乘
如果矩阵各列无关,则AtA可逆;
这里的最小二乘就是在AX = b的基础上左乘At,然后求X
17)正交矩阵和 Gram-Schmidt 正交化
标准正交的长度为1。
标准正交矩阵有:QtQ = I 于是可以得到Qt = Q-1,千万不要忘了单位化。
Gram - Schmidt正交化:联想到投影,不断减去投影的分量(看note……有点难描述),最后再进行单位化就好,比如三个正交向量a,b,c要施密特正交化; b可以减去在a上面的投影然后单位化,c要减去在a的投影和在b的投影然后再进行单位化。
18,19)行列式介绍
行列式的线性反应在每一行上,所以不会有个det(A + B) = det(A)+ det(B)
20)克莱姆法则、逆矩阵、体积
代数余子式 Ct = det(A)*A^-1(注意是转置,细节看note)
克莱姆法则:分母是行列式的值,分子是行列式换对应列。
体积 = 行列式的绝对值
21)特征值和特征向量
特征值之和与迹相等|特征值之积等于行列式的值
对称矩阵的特征值为诗书,反对称矩阵的特征值为虚数
22)对角化和A的幂
对角化:AX = X*diag
对角化的条件:矩阵一定要有n个线性无关的特征向量❗️
(如果矩阵A没有重复特征值,那么就一定有n个线性无关的特征向量;但是如果有重复的特征值,结论不是完全否定的)
23)微分方程和exp(At)
留个🕳️
24)马尔可夫矩阵和傅立叶级数
留个🕳️
25)复习二
26)对称矩阵及正定性(positive-definite)
对称矩阵特征值为实数:取转置共轭然后构造
正定矩阵就是一类对称矩阵满足:
(1)所有的特征值是正数
(2)所有主元为正
(3)所有的子行列式都为正
27)复数矩阵和快速傅立叶变换
🕳️🕳️
28)正定矩阵和最小值
正定矩阵判定:有四种方法(满足其一即可)
1️⃣特征值皆为正数(>0)
2️⃣顺序主子式均为正值
3️⃣主元均为正数
4️⃣判别式(xtAx > 0)
